Pierwsza dziesiątka systemu dziesiętnego w systemie dwójkowym wygląda tak:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010.
Proszę zauważyć, że do przesłania tych liczb np. przy pomocy impulsów światła (na zasadzie: zero brak błysku, jeden jest błysk – zgodnie z zasadą wyłączone/włączone) wystarczy prosty schemat. Zakodowanie liczb układu dziesiętnego nie byłoby tak proste.
Można też użyć np. alfabetu Morse’a. (kropka – zero, kreska – jeden).
A jak wykorzystać system dwójkowy do budowy prostego urządzenia szyfrującego? Przy okazji rozmawiając o kryptografii? Kryptografią określa się rozmaite procesy kodowania informacji. Zwykle rozumiemy pod tym pojęciem czynności, które prowadzą do transformacji jawnej formy wiadomości w formę ukrytą, zazwyczaj w celu uniemożliwienia dostępu do przekazywanych informacji osobom trzecim. Kodowanie wiadomości stosowano od bardzo dawnych czasów a sposoby na ukrywanie informacji wraz z rozwojem nauki i techniki stawały się coraz doskonalsze. Stosowano różne techniki do zaszyfrowania tajnych danych i informacji: od specjalnie wymyślanych alfabetów (w których czasem po prostu przestawiano kolejność liter alfabetu tradycyjnie stosowanego), przez zatrudnianie osób operujących rzadkimi i oryginalnymi językami (specjalnie przeszkoleni operatorzy, pochodzący np. z indiańskich plemion posługujący się słowami z mało znanych indiańskich dialektów) po nowoczesne techniki wykorzystujące zaawansowane techniki komputerowe oparte na systemie binarnym (zerojedynkowym). W szyfrowanie i odszyfrowanie bawił się prawie każdy, kto tylko chciał koniecznie (choćby podczas zabawy) przekazać ważne informacje drugiej osobie, bez wtajemniczania innych…
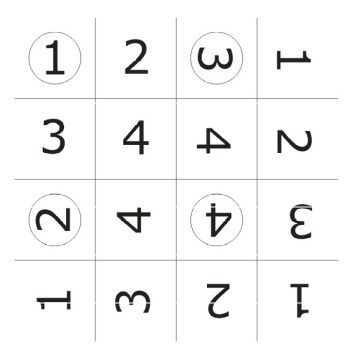
Urządzenie szyfrujące to zespół trzech szablonów, w których rozkład otworów kodujących został określony w systemie dwójkowym. Ponieważ każdy szablon jest kwadratem o proporcjach 4 x 4 (małe kwadraty - segmenty), ich rozkład można zapisać w systemie zero jedynkowym, pamiętając, że np. segmenty pełne szablonu to zero, a wycięte – jeden. I tak ustawiając szablony w pozycji wyjściowej (z otworem w segmencie umieszczonym w lewym, górnym rogu), czytając rzędami będziemy mieli następujące liczby: 1010, 0000, 1010, 0000. Na początek można wyciąć pojedynczy szablon i na nim przećwiczyć kodowanie informacji. Podczas szyfrowania należy wpisywać litery w poszczególne pola, obracać szablon o 90 stopni zgodnie z ruchem wskazówek zegara, wpisywać następne litery i tak Az do wykonania przez szablon obrotu o 360 stopni. Ta sama zasada dotyczy kodowania przy pomocy zespołu trzech szablonów. Należy tylko pamiętać, że obracamy wszystkie – po wypełnieniu pól literami. Litery wpisujemy rzędami utworzonymi przez trzy szablony (w każdym z czterech ustawień mamy zatem do dyspozycji po dwa rzędy pół po sześć liter każdy). Stworzony w ten sposób blok liter można odczytać analogicznie jak podczas zapisu – używając szablonów szyfrujących. Układ otworów w szablonach można zaprojektować na kilka sposobów. Należy jednak uważać, żeby pola nie trafiały na siebie podczas obracania szablonu. Dla łatwiejszego projektowania szablonów szyfrujących można posłużyć się graficznym schematem.
Okienka wycinamy wybierając cztery dowolne pola, uważając tylko na to, żeby nie wybierać takich samych numerów… proste? Na schemacie zaznaczone są okienka rozplanowane w modelu, który prezentowany jest w tym scenariuszu.
Co ciekawe szablon o proporcjach cztery na cztery segmenty (16 pól) można skomponować na 256 różnych układów. Gdyby użyć kwadratu o proporcjach osiem na osiem (16 okienek szyfrujących) możliwych układów byłoby… ponad cztery miliardy, czyli cztery do szesnastej potęgi.
Szablony do urządzenia szyfrującego są umieszczone na trzech kołach umieszczonych w jednej linii i zachodzących na siebie. Należy je umocować w panelu z wycięciami, w których będą mogły się obracać, tworząc jeden układ.
Projekt zrealizowany przez Stowarzyszenie Ars Scientia. Film powstał przy dofinansowaniu Fundacji MBanku.
A jak wykorzystać system dwójkowy do budowy prostego urządzenia szyfrującego? Przy okazji rozmawiając o kryptografii? Kryptografią określa się rozmaite procesy kodowania informacji. Zwykle rozumiemy pod tym pojęciem czynności, które prowadzą do transformacji jawnej formy wiadomości w formę ukrytą, zazwyczaj w celu uniemożliwienia dostępu do przekazywanych informacji osobom trzecim. Kodowanie wiadomości stosowano od bardzo dawnych czasów a sposoby na ukrywanie informacji wraz z rozwojem nauki i techniki stawały się coraz doskonalsze. Stosowano różne techniki do zaszyfrowania tajnych danych i informacji: od specjalnie wymyślanych alfabetów (w których czasem po prostu przestawiano kolejność liter alfabetu tradycyjnie stosowanego), przez zatrudnianie osób operujących rzadkimi i oryginalnymi językami (specjalnie przeszkoleni operatorzy, pochodzący np. z indiańskich plemion posługujący się słowami z mało znanych indiańskich dialektów) po nowoczesne techniki wykorzystujące zaawansowane techniki komputerowe oparte na systemie binarnym (zerojedynkowym). W szyfrowanie i odszyfrowanie bawił się prawie każdy, kto tylko chciał koniecznie (choćby podczas zabawy) przekazać ważne informacje drugiej osobie, bez wtajemniczania innych…
Urządzenie szyfrujące to zespół trzech szablonów, w których rozkład otworów kodujących został określony w systemie dwójkowym. Ponieważ każdy szablon jest kwadratem o proporcjach 4 x 4 (małe kwadraty - segmenty), ich rozkład można zapisać w systemie zero jedynkowym, pamiętając, że np. segmenty pełne szablonu to zero, a wycięte – jeden. I tak ustawiając szablony w pozycji wyjściowej (z otworem w segmencie umieszczonym w lewym, górnym rogu), czytając rzędami będziemy mieli następujące liczby: 1010, 0000, 1010, 0000. Na początek można wyciąć pojedynczy szablon i na nim przećwiczyć kodowanie informacji. Podczas szyfrowania należy wpisywać litery w poszczególne pola, obracać szablon o 90 stopni zgodnie z ruchem wskazówek zegara, wpisywać następne litery i tak Az do wykonania przez szablon obrotu o 360 stopni. Ta sama zasada dotyczy kodowania przy pomocy zespołu trzech szablonów. Należy tylko pamiętać, że obracamy wszystkie – po wypełnieniu pól literami. Litery wpisujemy rzędami utworzonymi przez trzy szablony (w każdym z czterech ustawień mamy zatem do dyspozycji po dwa rzędy pół po sześć liter każdy). Stworzony w ten sposób blok liter można odczytać analogicznie jak podczas zapisu – używając szablonów szyfrujących. Układ otworów w szablonach można zaprojektować na kilka sposobów. Należy jednak uważać, żeby pola nie trafiały na siebie podczas obracania szablonu. Dla łatwiejszego projektowania szablonów szyfrujących można posłużyć się graficznym schematem.
Okienka wycinamy wybierając cztery dowolne pola, uważając tylko na to, żeby nie wybierać takich samych numerów… proste? Na schemacie zaznaczone są okienka rozplanowane w modelu, który prezentowany jest w tym scenariuszu.
Co ciekawe szablon o proporcjach cztery na cztery segmenty (16 pól) można skomponować na 256 różnych układów. Gdyby użyć kwadratu o proporcjach osiem na osiem (16 okienek szyfrujących) możliwych układów byłoby… ponad cztery miliardy, czyli cztery do szesnastej potęgi.
Szablony do urządzenia szyfrującego są umieszczone na trzech kołach umieszczonych w jednej linii i zachodzących na siebie. Należy je umocować w panelu z wycięciami, w których będą mogły się obracać, tworząc jeden układ.
Projekt zrealizowany przez Stowarzyszenie Ars Scientia. Film powstał przy dofinansowaniu Fundacji MBanku.